Geometry

Geometry#

The IGA concept relies on the fact that the geometry (domain) is divided into subdomains, and each of these subdomains is the image of a Line, Square or a Cube by a geometric transformation (also called a mapping), that we shall call a patch or logical domain.

The following example shows a domain (half of annulus) that is the image of a logical domain using the mapping F. Each element (or cell) \(Q\) of the logical domain is then mapped into an element \(K\) of our domain, i.e. \(K = \mathbf{F}(Q)\).

png

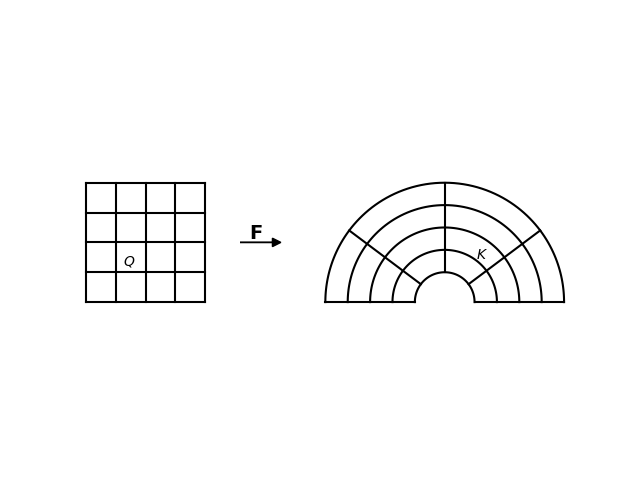
Coordinates in the logical domain are defined by the variables \(\left( x_1, x_2, x_3 \right)\) while the physical coordinates are denoted by \(\left( x,y,z \right)\).

How to define a geometry?#

Depending on your problem, you can be in one of the following situations;

  • your geometry is trivial, i.e. it is a Line, Square or a Cube. In this case, just use the SymPDE adhoc constructors, for which you’ll define the bounds.

  • your geometry can be defined using an Analytical Mapping. See the next section.

  • your geometry can be defined using a Discrete Mapping. See the next sections.

Contents